Page 152 - Mitja Sardoč, Igor Ž. Žagar in Ana Mlekuž, ur. ▪︎ Raziskovanje v vzgoji in izobraževanju. Ljubljana: Pedagoški inštitut, 2018. Digitalna knjižnica, Dissertationes 26

r aziskovanje v vzgoji in izobr aževanju

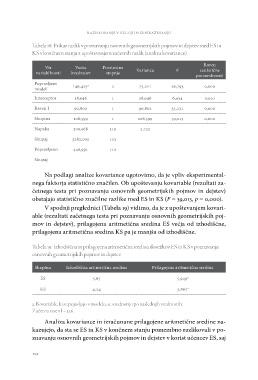
Tabela 18: Prikaz razlik v poznavanju osnovnih geometrijskih pojmov in dejstev med ES in
KS v končnem stanju z upoštevanjem začetnih razlik (analiza kovariance)

Vir Vsota Prostostne Varianca F Raven
variabilnosti kvadratov stopnje statistične
Popravljeni 73,211 26,793 pomembnosti
model 146,423a 2 18,946 6,934
Interceptor 18,946 1 90,802 33,231 0,000
Raven I 90,802 1 106,599 39,013
Skupina 106,599 1 2,732 0,010
Napaka 300,568 110 0,000
Skupaj 3282,000 113 0,000
Popravljeno 446,991 112
Skupaj

Na podlagi analize kovariance ugotovimo, da je vpliv eksperimental-
nega faktorja statistično značilen. Ob upoštevanju kovariable (rezultati za-
četnega testa pri poznavanju osnovnih geometrijskih pojmov in dejstev)
obstajajo statistično značilne razlike med ES in KS (F = 39,013, p = 0,000).

V spodnji preglednici (Tabela 19) vidimo, da je z upoštevanjem kovari-
able (rezultati začetnega testa pri poznavanju osnovnih geometrijskih poj-
mov in dejstev), prilagojena aritmetična sredina ES večja od izhodiščne,
prilagojena aritmetična sredina KS pa je manjša od izhodiščne.

Tabela 19: Izhodiščna in prilagojena aritmetična sredina dosežkov ES in KS v poznavanju
osnovnih geometrijskih pojmov in dejstev

Skupina Izhodiščna aritmetična sredina Prilagojena aritmetična sredina
ES 5,65 5,949a
KS 4,24 3,865a

a. Kovariable, ki se pojavljajo v modelu, se vrednotijo po naslednjih vrednostih:
Začetna raven I = 5,56.

Analiza kovariance in izračunane prilagojene aritmetične sredine na-
kazujejo, da sta se ES in KS v končnem stanju pomembno razlikovali v po-
znavanju osnovnih geometrijskih pojmov in dejstev v korist učencev ES, saj

152