Page 157 - Ana Mlekuž in Igor Ž. Žagar, ur. • Raziskovanje v vzgoji in izobraževanju: Digitalizacija vzgoje in izobraževanja – priložnosti in pasti. Ljubljana: Pedagoški inštitut, 2023. Digitalna knjižnica, Dissertationes 46
P. 157
otavljanje k akovosti pr i vr ednotenju pr eizkusov nacionalnega pr everjanja znanja
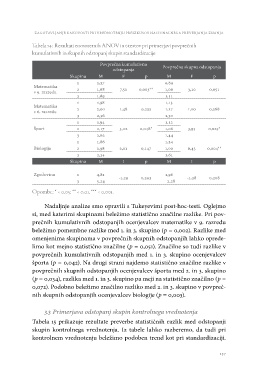
Tabela 14: Rezultati enosmernih ANOV in t-testov pri primerjavi povprečnih
kumulativnih in skupnih odstopanj skupin standardizacije
Povprečna kumulativna Povprečna skupna odstopanja
odstopanja
MF p
Skupina MF p 0,89
1 1,06 3,10 0,051
Matematika 2 1,37 1,11
v 9. razredu 3 1,13
Matematika 1 1,68 7,51 0,003** 1,17 1,00 0,368
v 6. razredu 2 1,30
Šport 3 1,89 1,12
1 1,06 3,95 0,025*
Biologija 2 1,98 1,44
3 1,24
1 2,00 1,48 0,233 1,00 6,43 0,004**
2 1,61
3 2,36 Mt p
Skupina 1,94
2,17 3,22 0,048*
2,62
1,86
1,98 2,01 0,147
2,34
Mt p
Zgodovina 1 4,81 -1,29 0,203 1,96 -1,28 0,208
3 5,24 2,28
Opombe: * < 0,05; ** < 0,01, *** < 0,001.
Nadaljnje analize smo opravili s Tukeyevimi post-hoc-testi. Oglejmo
si, med katerimi skupinami beležimo statistično značilne razlike. Pri pov-
prečnih kumulativnih odstopanjih ocenjevalcev matematike v 9. razredu
beležimo pomembne razlike med 1. in 3. skupino (p = 0,002). Razlike med
omenjenima skupinama v povprečnih skupnih odstopanjih lahko oprede-
limo kot mejno statistično značilne (p = 0,051). Značilne so tudi razlike v
povprečnih kumulativnih odstopanjih med 1. in 3. skupino ocenjevalcev
športa (p = 0,042). Na drugi strani najdemo statistično značilne razlike v
povprečnih skupnih odstopanjih ocenjevalcev športa med 2. in 3. skupino
(p = 0,034), razlika med 1. in 3. skupino pa meji na statistično značilno (p =
0,072). Podobno beležimo značilno razliko med 2. in 3. skupino v povpreč-
nih skupnih odstopanjih ocenjevalcev biologije (p = 0,003).
3.3 Primerjava odstopanj skupin kontrolnega vrednotenja
Tabela 15 prikazuje rezultate preverbe statističnih razlik med odstopanji
skupin kontrolnega vrednotenja. Iz tabele lahko razberemo, da tudi pri
kontrolnem vrednotenju beležimo podoben trend kot pri standardizaciji.
157
Tabela 14: Rezultati enosmernih ANOV in t-testov pri primerjavi povprečnih
kumulativnih in skupnih odstopanj skupin standardizacije
Povprečna kumulativna Povprečna skupna odstopanja
odstopanja
MF p
Skupina MF p 0,89
1 1,06 3,10 0,051
Matematika 2 1,37 1,11
v 9. razredu 3 1,13
Matematika 1 1,68 7,51 0,003** 1,17 1,00 0,368
v 6. razredu 2 1,30
Šport 3 1,89 1,12
1 1,06 3,95 0,025*
Biologija 2 1,98 1,44
3 1,24
1 2,00 1,48 0,233 1,00 6,43 0,004**
2 1,61
3 2,36 Mt p
Skupina 1,94
2,17 3,22 0,048*
2,62
1,86
1,98 2,01 0,147
2,34
Mt p
Zgodovina 1 4,81 -1,29 0,203 1,96 -1,28 0,208
3 5,24 2,28
Opombe: * < 0,05; ** < 0,01, *** < 0,001.
Nadaljnje analize smo opravili s Tukeyevimi post-hoc-testi. Oglejmo
si, med katerimi skupinami beležimo statistično značilne razlike. Pri pov-
prečnih kumulativnih odstopanjih ocenjevalcev matematike v 9. razredu
beležimo pomembne razlike med 1. in 3. skupino (p = 0,002). Razlike med
omenjenima skupinama v povprečnih skupnih odstopanjih lahko oprede-
limo kot mejno statistično značilne (p = 0,051). Značilne so tudi razlike v
povprečnih kumulativnih odstopanjih med 1. in 3. skupino ocenjevalcev
športa (p = 0,042). Na drugi strani najdemo statistično značilne razlike v
povprečnih skupnih odstopanjih ocenjevalcev športa med 2. in 3. skupino
(p = 0,034), razlika med 1. in 3. skupino pa meji na statistično značilno (p =
0,072). Podobno beležimo značilno razliko med 2. in 3. skupino v povpreč-
nih skupnih odstopanjih ocenjevalcev biologije (p = 0,003).
3.3 Primerjava odstopanj skupin kontrolnega vrednotenja
Tabela 15 prikazuje rezultate preverbe statističnih razlik med odstopanji
skupin kontrolnega vrednotenja. Iz tabele lahko razberemo, da tudi pri
kontrolnem vrednotenju beležimo podoben trend kot pri standardizaciji.
157