Page 158 - Ana Mlekuž in Igor Ž. Žagar, ur. • Raziskovanje v vzgoji in izobraževanju: Digitalizacija vzgoje in izobraževanja – priložnosti in pasti. Ljubljana: Pedagoški inštitut, 2023. Digitalna knjižnica, Dissertationes 46
P. 158
r aziskovanje v vzgoji in izobr aževanju: digitalizacija vzgoje in izobr aževanja ...
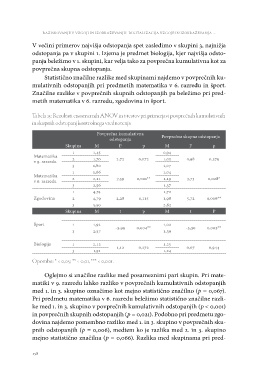
V večini primerov najvišja odstopanja spet zasledimo v skupini 3, najnižja
odstopanja pa v skupini 1. Izjema je predmet biologija, kjer najvišja odsto-
panja beležimo v 1. skupini, kar velja tako za povprečna kumulativna kot za
povprečna skupna odstopanja.
Statistično značilne razlike med skupinami najdemo v povprečnih ku-
mulativnih odstopanjih pri predmetih matematika v 6. razredu in šport.
Značilne razlike v povprečnih skupnih odstopanjih pa beležimo pri pred-
metih matematika v 6. razredu, zgodovina in šport.
Tabela 15: Rezultati enosmernih ANOV in t-testov pri primerjavi povprečnih kumulativnih
in skupnih odstopanj kontrolnega vrednotenja
Povprečna kumulativna Povprečna skupna odstopanja
odstopanja
Skupina MF p MF p
1
Matematika 2 1,45 0,94
v 9. razredu 3
Matematika 1 1,70 2,72 0,072 1,05 0,98 0,379
v 6. razredu 2
Zgodovina 3 1,80 1,07
1
2 1,66 1,04
3
2,11 7,39 0,001** 1,19 3,73 0,028*
Skupina
2,56 1,37
4,74 1,72
4,79 2,28 0,115 1,98 5,72 0,006**
5,50 2,62
Mt p Mt P
Šport 1 1,92 -2,99 0,004** 1,02 -3,30 0,002**
3 2,57 1,39
Biologija 1 2,12 1,12 0,272 1,25 0,07 0,944
3 1,91 1,24
Opombe: * < 0,05; ** < 0,01, *** < 0,001.
Oglejmo si značilne razlike med posameznimi pari skupin. Pri mate-
matiki v 9. razredu lahko razliko v povprečnih kumulativnih odstopanjih
med 1. in 3. skupino označimo kot mejno statistično značilno (p = 0,067).
Pri predmetu matematika v 6. razredu beležimo statistično značilne razli-
ke med 1. in 3. skupino v povprečnih kumulativnih odstopanjih (p < 0,001)
in povprečnih skupnih odstopanjih (p = 0,021). Podobno pri predmetu zgo-
dovina najdemo pomembno razliko med 1. in 3. skupino v povprečnih sku-
pnih odstopanjih (p = 0,006), medtem ko je razlika med 2. in 3. skupino
mejno statistično značilna (p = 0,066). Razlika med skupinama pri pred-
158
V večini primerov najvišja odstopanja spet zasledimo v skupini 3, najnižja
odstopanja pa v skupini 1. Izjema je predmet biologija, kjer najvišja odsto-
panja beležimo v 1. skupini, kar velja tako za povprečna kumulativna kot za
povprečna skupna odstopanja.
Statistično značilne razlike med skupinami najdemo v povprečnih ku-
mulativnih odstopanjih pri predmetih matematika v 6. razredu in šport.
Značilne razlike v povprečnih skupnih odstopanjih pa beležimo pri pred-
metih matematika v 6. razredu, zgodovina in šport.
Tabela 15: Rezultati enosmernih ANOV in t-testov pri primerjavi povprečnih kumulativnih
in skupnih odstopanj kontrolnega vrednotenja
Povprečna kumulativna Povprečna skupna odstopanja
odstopanja
Skupina MF p MF p
1
Matematika 2 1,45 0,94
v 9. razredu 3
Matematika 1 1,70 2,72 0,072 1,05 0,98 0,379
v 6. razredu 2
Zgodovina 3 1,80 1,07
1
2 1,66 1,04
3
2,11 7,39 0,001** 1,19 3,73 0,028*
Skupina
2,56 1,37
4,74 1,72
4,79 2,28 0,115 1,98 5,72 0,006**
5,50 2,62
Mt p Mt P
Šport 1 1,92 -2,99 0,004** 1,02 -3,30 0,002**
3 2,57 1,39
Biologija 1 2,12 1,12 0,272 1,25 0,07 0,944
3 1,91 1,24
Opombe: * < 0,05; ** < 0,01, *** < 0,001.
Oglejmo si značilne razlike med posameznimi pari skupin. Pri mate-
matiki v 9. razredu lahko razliko v povprečnih kumulativnih odstopanjih
med 1. in 3. skupino označimo kot mejno statistično značilno (p = 0,067).
Pri predmetu matematika v 6. razredu beležimo statistično značilne razli-
ke med 1. in 3. skupino v povprečnih kumulativnih odstopanjih (p < 0,001)
in povprečnih skupnih odstopanjih (p = 0,021). Podobno pri predmetu zgo-
dovina najdemo pomembno razliko med 1. in 3. skupino v povprečnih sku-
pnih odstopanjih (p = 0,006), medtem ko je razlika med 2. in 3. skupino
mejno statistično značilna (p = 0,066). Razlika med skupinama pri pred-
158