Page 84 - Maša Vidmar, Vedenjske težave in učna uspešnost. Ljubljana: Pedagoški inštitut, 2017. Digitalna knjižnica, Dissertationes, 30
P. 84
vedenjske težave in učna uspešnost
SRMR, rezultati so prikazani v tabeli 5. Natančne nasičenosti označevalcev
in drugi parametri za vsako KFA so na voljo v arhivu pri avtorici.
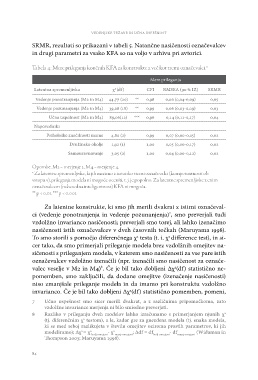
Tabela 4: Mere prileganja končnih KFA za konstrukte z več kot tremi označevalci.a
Mere prileganja
Latentna spremenljivka χ2 (df) CFI RMSEA (90 % IZ) SRMR
0,05
Vedenje ponotranjenja (M2 in M4) 44,77 (20) ** 0,98 0,06 (0,04-0,09) 0,03
0,06 (0,03-0,09) 0,04
Vedenje pozunanjenja (M2 in M4) 39,08 (18) ** 0,99 0,14 (0,11-0,17)
0,02
Učna uspešnost (M2 in M4) 89,06(12) *** 0,96 0,07 (0,00-0,15) 0,02
0,05 (0,00-0,17) 0,02
Napovedniki 0,04 (0,00-0,12)
Psihološke značilnosti mame 4,80 (2) 0,99
Družinsko okolje 1,92 (1) 1,00
Samouravnavanje 3,05 (2) 1,00
Opombe. M2 = merjenje 2, M4 = merjenje 4.
a Za latentne spremenljivke, ki jih merimo z natanko tremi označevalci (kompetentnosti ob
vstopu v), prileganja modela ni mogoče oceniti, t. j. je popolno. Za latentne spremenljivke z enim
označevalcem (nebesedna inteligentnost) KFA ni mogoča.
** p < 0,01, *** p < 0,001.
Za latentne konstrukte, ki smo jih merili dvakrat z istimi označeval-
ci (vedenje ponotranjenja in vedenje pozunanjenja)7, smo preverjali tudi
vzdolžno invarianco nasičenosti; preverjali smo torej, ali lahko izenačimo
nasičenosti istih označevalcev v dveh časovnih točkah (Maruyama 1998).
To smo storili s pomočjo diferenčnega χ2 testa (t. i. χ2 difference test), in si-
cer tako, da smo primerjali prileganje modela brez vzdolžnih omejitev na-
sičenosti s prileganjem modela, v katerem smo nasičenosti za vse pare istih
označevalcev vzdolžno izenačili (npr. izenačili smo nasičenost za označe-
valec veselje v M2 in M4)8. Če je bil tako dobljeni Δχ2(df) statistično ne-
pomemben, smo zaključili, da dodane omejitve (izenačenje nasičenosti)
niso zmanjšale prileganje modela in da imamo pri konstruktu vzdolžno
invarianco. Če je bil tako dobljeni Δχ2(df) statistično pomemben, pomeni,
7 Učno uspešnost smo sicer merili dvakrat, a z različnima pripomočkoma, zato
vzdolžne invariance merjenja ni bilo smiselno preverjati.
8 Razliko v prileganju dveh modelov lahko izračunamo s primerjanjem njunih χ2
(tj. diferenčnim χ2 testom), a le, kadar gre za gnezdena modela (tj. enaka modela,
ki se med seboj razlikujeta v številu omejitev oziroma prostih parametrov, ki jih
mThoodmelpirsaomn o2)0;0Δ3χ; 2M=aχr2uboyljaommejaeni1-9χ928m)a.nj ;omejeni Δdf = df bolj -omejeni dfmanj omejeni (Widaman in
84
SRMR, rezultati so prikazani v tabeli 5. Natančne nasičenosti označevalcev
in drugi parametri za vsako KFA so na voljo v arhivu pri avtorici.
Tabela 4: Mere prileganja končnih KFA za konstrukte z več kot tremi označevalci.a
Mere prileganja
Latentna spremenljivka χ2 (df) CFI RMSEA (90 % IZ) SRMR
0,05
Vedenje ponotranjenja (M2 in M4) 44,77 (20) ** 0,98 0,06 (0,04-0,09) 0,03
0,06 (0,03-0,09) 0,04
Vedenje pozunanjenja (M2 in M4) 39,08 (18) ** 0,99 0,14 (0,11-0,17)
0,02
Učna uspešnost (M2 in M4) 89,06(12) *** 0,96 0,07 (0,00-0,15) 0,02
0,05 (0,00-0,17) 0,02
Napovedniki 0,04 (0,00-0,12)
Psihološke značilnosti mame 4,80 (2) 0,99
Družinsko okolje 1,92 (1) 1,00
Samouravnavanje 3,05 (2) 1,00
Opombe. M2 = merjenje 2, M4 = merjenje 4.
a Za latentne spremenljivke, ki jih merimo z natanko tremi označevalci (kompetentnosti ob
vstopu v), prileganja modela ni mogoče oceniti, t. j. je popolno. Za latentne spremenljivke z enim
označevalcem (nebesedna inteligentnost) KFA ni mogoča.
** p < 0,01, *** p < 0,001.
Za latentne konstrukte, ki smo jih merili dvakrat z istimi označeval-
ci (vedenje ponotranjenja in vedenje pozunanjenja)7, smo preverjali tudi
vzdolžno invarianco nasičenosti; preverjali smo torej, ali lahko izenačimo
nasičenosti istih označevalcev v dveh časovnih točkah (Maruyama 1998).
To smo storili s pomočjo diferenčnega χ2 testa (t. i. χ2 difference test), in si-
cer tako, da smo primerjali prileganje modela brez vzdolžnih omejitev na-
sičenosti s prileganjem modela, v katerem smo nasičenosti za vse pare istih
označevalcev vzdolžno izenačili (npr. izenačili smo nasičenost za označe-
valec veselje v M2 in M4)8. Če je bil tako dobljeni Δχ2(df) statistično ne-
pomemben, smo zaključili, da dodane omejitve (izenačenje nasičenosti)
niso zmanjšale prileganje modela in da imamo pri konstruktu vzdolžno
invarianco. Če je bil tako dobljeni Δχ2(df) statistično pomemben, pomeni,
7 Učno uspešnost smo sicer merili dvakrat, a z različnima pripomočkoma, zato
vzdolžne invariance merjenja ni bilo smiselno preverjati.
8 Razliko v prileganju dveh modelov lahko izračunamo s primerjanjem njunih χ2
(tj. diferenčnim χ2 testom), a le, kadar gre za gnezdena modela (tj. enaka modela,
ki se med seboj razlikujeta v številu omejitev oziroma prostih parametrov, ki jih
mThoodmelpirsaomn o2)0;0Δ3χ; 2M=aχr2uboyljaommejaeni1-9χ928m)a.nj ;omejeni Δdf = df bolj -omejeni dfmanj omejeni (Widaman in
84