Page 267 - Gabrijela Kišiček and Igor Ž. Žagar (eds.), What do we know about the world? Rhetorical and argumentative perspectives, Digital Library, Educational Research Institute, Ljubljana 2013
P. 267
taking judges seriously 267
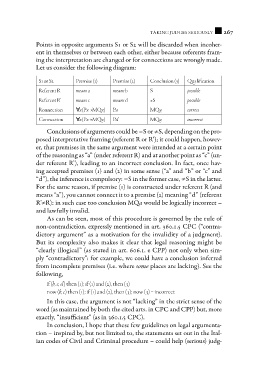
Points in opposite arguments S1 or S2 will be discarded when incoher-
ent in themselves or between each other, either because referents fram-
ing the interpretation are changed or for connections are wrongly made.
Let us consider the following diagram:
S1 or S2 Premise (1) Premise (2) Conclusion (3) Qualification
Referent R means a means b S possible
Referent R’ means c means d ≠S possible
Ronnection "x(Px →MQx) Pa MQa correct
Connection "x(Px →MQx) Pd MQa incorrect
Conclusions of arguments could be =S or ≠S, depending on the pro-
posed interpretative framing (referent R or R’); it could happen, howev-
er, that premises in the same argument were intended at a certain point
of the reasoning as “a” (under referent R) and at another point as “c” (un-
der referent R’), leading to an incorrect conclusion. In fact, once hav-
ing accepted premises (1) and (2) in some sense (“a” and “b” or “c” and
“d”), the inference is compulsory: =S in the former case, ≠S in the latter.
For the same reason, if premise (1) is constructed under referent R (and
means “a”), you cannot connect it to a premise (2) meaning “d” (referent
R’≠R): in such case too conclusion MQa would be logically incorrect –
and lawfully invalid.
As can be seen, most of this procedure is governed by the rule of
non-contradiction, expressly mentioned in art. 360.1.5 CPC (“contra-
dictory argument” as a motivation for the invalidity of a judgment).
But its complexity also makes it clear that legal reasoning might be
“clearly illogical” (as stated in art. 606.1. e CPP) not only when sim-
ply “contradictory”: for example, we could have a conclusion inferred
from incomplete premises (i.e. where some places are lacking). See the
following,
if (b, c, d) then (1); if (1) and (2), then (3)
now (b, c) then (1); if (1) and (2), then (3); now (3) = incorrect
In this case, the argument is not “lacking” in the strict sense of the
word (as maintained by both the cited arts. in CPC and CPP) but, more
exactly, “insufficient” (as in 360.1.5 CPC).
In conclusion, I hope that these few guidelines on legal argumenta-
tion – inspired by, but not limited to, the statements set out in the Ital-
ian codes of Civil and Criminal procedure – could help (serious) judg-
Points in opposite arguments S1 or S2 will be discarded when incoher-
ent in themselves or between each other, either because referents fram-
ing the interpretation are changed or for connections are wrongly made.
Let us consider the following diagram:
S1 or S2 Premise (1) Premise (2) Conclusion (3) Qualification
Referent R means a means b S possible
Referent R’ means c means d ≠S possible
Ronnection "x(Px →MQx) Pa MQa correct
Connection "x(Px →MQx) Pd MQa incorrect
Conclusions of arguments could be =S or ≠S, depending on the pro-
posed interpretative framing (referent R or R’); it could happen, howev-
er, that premises in the same argument were intended at a certain point
of the reasoning as “a” (under referent R) and at another point as “c” (un-
der referent R’), leading to an incorrect conclusion. In fact, once hav-
ing accepted premises (1) and (2) in some sense (“a” and “b” or “c” and
“d”), the inference is compulsory: =S in the former case, ≠S in the latter.
For the same reason, if premise (1) is constructed under referent R (and
means “a”), you cannot connect it to a premise (2) meaning “d” (referent
R’≠R): in such case too conclusion MQa would be logically incorrect –
and lawfully invalid.
As can be seen, most of this procedure is governed by the rule of
non-contradiction, expressly mentioned in art. 360.1.5 CPC (“contra-
dictory argument” as a motivation for the invalidity of a judgment).
But its complexity also makes it clear that legal reasoning might be
“clearly illogical” (as stated in art. 606.1. e CPP) not only when sim-
ply “contradictory”: for example, we could have a conclusion inferred
from incomplete premises (i.e. where some places are lacking). See the
following,
if (b, c, d) then (1); if (1) and (2), then (3)
now (b, c) then (1); if (1) and (2), then (3); now (3) = incorrect
In this case, the argument is not “lacking” in the strict sense of the
word (as maintained by both the cited arts. in CPC and CPP) but, more
exactly, “insufficient” (as in 360.1.5 CPC).
In conclusion, I hope that these few guidelines on legal argumenta-
tion – inspired by, but not limited to, the statements set out in the Ital-
ian codes of Civil and Criminal procedure – could help (serious) judg-