Page 265 - Igor Ž. Žagar in Ana Mlekuž, ur. Raziskovanje v vzgoji in izobraževanju: mednarodni vidiki vzgoje in izobraževanja. Ljubljana: Pedagoški inštitut, 2020. Digitalna knjižnica, Dissertationes 38
P. 265
mathematical modelling in pr imary schools-advanced topics at elementary level
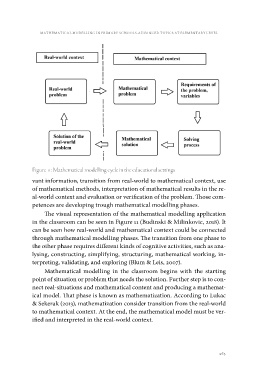
Figure 11: Mathematical modelling cycle in the educational settings
vant information, transition from real-world to mathematical context, use
of mathematical methods, interpretation of mathematical results in the re-
al-world context and evaluation or verification of the problem. Those com-
petences are developing trough mathematical modelling phases.
The visual representation of the mathematical modelling application
in the classroom can be seen in Figure 11 (Budinski & Milinkovic, 2018). It
can be seen how real-world and mathematical context could be connected
through mathematical modelling phases. The transition from one phase to
the other phase requires different kinds of cognitive activities, such as ana-
lysing, constructing, simplifying, structuring, mathematical working, in-
terpreting, validating, and exploring (Blum & Leis, 2007).
Mathematical modelling in the classroom begins with the starting
point of situation or problem that needs the solution. Further step is to con-
nect real-situations and mathematical content and producing a mathemat-
ical model. That phase is known as mathematization. According to Lukac
& Sekerak (2013), mathematization consider transition from the real-world
to mathematical context. At the end, the mathematical model must be ver-
ified and interpreted in the real-world context.
265
Figure 11: Mathematical modelling cycle in the educational settings
vant information, transition from real-world to mathematical context, use
of mathematical methods, interpretation of mathematical results in the re-
al-world context and evaluation or verification of the problem. Those com-
petences are developing trough mathematical modelling phases.
The visual representation of the mathematical modelling application
in the classroom can be seen in Figure 11 (Budinski & Milinkovic, 2018). It
can be seen how real-world and mathematical context could be connected
through mathematical modelling phases. The transition from one phase to
the other phase requires different kinds of cognitive activities, such as ana-
lysing, constructing, simplifying, structuring, mathematical working, in-
terpreting, validating, and exploring (Blum & Leis, 2007).
Mathematical modelling in the classroom begins with the starting
point of situation or problem that needs the solution. Further step is to con-
nect real-situations and mathematical content and producing a mathemat-
ical model. That phase is known as mathematization. According to Lukac
& Sekerak (2013), mathematization consider transition from the real-world
to mathematical context. At the end, the mathematical model must be ver-
ified and interpreted in the real-world context.
265